Brincando de Matemática

Vou colocar algumas coisas curiosas, exóticas... melhor, umas brincadeirinhas que fazemos nas aulas de Cálculo, e nas fábulosas de Laboratório do Simon. E até ver como a matemática é dahora. Como por exemplo "provar as coisas absurdas". Se não tem o que fazer, está entediado na frente do PC ou da TV? Pegue um livro de Cálculo do Stewart ou Guidorizzi, e comece a brincar com a matemática, e verá como tal é maravilhosa.

Uma grande descoberta envolve a solução de um grande problema, mas há uma semente de descoberta na solução de qualquer problema. Seu problema pode ser modesto; porém, se ele desafiar sua curiosidade e fizer funcionar sua capacidade inventiva, e caso você o resolva sozinho, então você poderá experimentar a tensão e o prazer do triunfo da descoberta.

George Polya

Tentei mostrar as seguintes demonstrações e provas da forma mais simples possível, dentro dos recursos de texto do Blogger, mostrando passo-a-passo, para não mostrar dúvidas, esclarendo para qualquer um não acostumado em fazer contas. Bem, é isto, aproveite.


Encontrando a Fórmula de Bascara
Para quem pensava que uma pessoa do nada teve uma "visão do além", ou que sem querer, chutou uma fórmula, ou do nada um gênio, olhou uma estrutura da equação de segundo grau e desenvolveu uma fórmula infalivel etc. Bem, estaVAMOS enganados. Qualquer matemático um pouco mais treinado e persistente na algebra, consegue chegar nessa fórmula. Olha só como é feito.

temos uma f(x) = ax²+bx+c

Então vamos encontraras raizes dessa função, a partir dos coeficientes das variantes (x). Ou seja, como resolver a coisa, esquecendo que existe o x², em outras palavras, como achar o x apenas usando seus conficientes. Tal formula também funciona para as equações de primeira grau --> f(x) = ax + b. Porém, é fácil demais, e não precisa de um Bascara.

Resolvendo:

f(x)=ax²+bx+c = a[x² + (b/a)x] + c

Entendeu a passagem? Se multiplicarmos a por x²+(b/a)x teremos a mesma equação anterior: ax²+bx

é primordial entender essas passagens. Pois é assim que resolveremos toda equação.

continuando:
= a[x²+(b/a)x + b²/4a²] - a(b²/4a²) + c

f(x) = ax²+bx+c = a(x + b/2a)² - b²/4a + c

faze-se a passagem: [-b² + c (4a)] / 4a

f(x)= a(x + b/2a)² + [(-b² + 4ac)/4a] (isso começa a parecer familiar, não?)

f(x) = a(x + b/2a)² - D/4a ---> para D= delta

"lembra? Delta não é D, só que usando aquele triangulo? Tal que:
D = b² - 4ac"

Para encontramos a raiz de uma função, lembrem que temos que fazer y=f(x)=0. Então com isso temos:

f(x) = 0 = a(x + b/2a)² - D/4a

=> a(x + b/2a)² = D/4a --> passe o a, multiplicando 4a

Tirando a RAIZ quadrada dos dois lados... teremos: para *{ a} = raiz quadrada de a

*{(x+b/2a)²} = +- *{D/4a²}

=> x + b/2a = +- *{D}/2a

(já está bem familiar, não? Estamos quase lá.)

Isolando o X:

x = -b/2a +- *{D}/2a

Então chegamos a fórmula de Bascara.

x = (-b +- *{D}) / 2a)

Ou seja,

Para f(x) = ax²+bx + c
Temos para f(x)=o:
x = (-b +- *{d})/a

ou melhor

x = -b +- *{D}
........_____________
.............2a


Lembrou?


.........
Bem, é isto. E foi daí que temos essa fórmula. Patenteada por Bascara. Pois tal foi a primeira pessoa que resolveu isto.

Expliquei o mais claro possivel, de forma bem simples. Talvez complique pois aqui no PC só dá para usar uma linha, o que deixa pouco nitido as divisões. Em caso de dúvidas, tente passar para um papel.

.......

Provando que 1 =/ 0 (1 é diferente de zero)

Absurdo? É realmente, é um absurdo. Mas por que é um absurdo? Bem, temos que PROVAR que 1 =/ 0, matemáticamente. E como? Vamos provar por absurdo.

Procar por absurdo: é nós negarmos a tese. Ou seja, fazermos caso não fosse verdade (o contrário). Então, se a resolução demonstrar um absurdo de tal forma que tudo fique incoerente. Então é porque realmente, aquilo era verdade. Então, se negando a tese seria um absurdo, então dessa forma provamos que era verdade.

Então, vamos provar por absurdo que 1 =/ 0

Neguemos a tese. Então vamos dizer que 1=0.

Sabemos das propriedades do CORPO dos números Reais. ENtão vamos usá-las. Que propriedades são essas? Fácil! Com certeza você é o maior craque em usá-las.

Como apenas usaremos as propriedades da Adição, vou apenas colocá-las:

A1 = Associativa --> (x + y) + z = x + (y + z)
A2 = Comutativa --> x + y = y + x
A3 = Elemento Neutro --> x + 0 = x
A4 = Oposto --> Para todo a, existe um (-a), tal que, a + (-a) = 0

São essas as propriedades do corpo. Ridiculo não? Se quiser, até dá para provar tais.

ENtão voltando ao nosso problema. Vamos provar que 0=1.

Vamos usar a A3. Se 1=0, então podemos usar 0=1, pela propriedade A2.

=> (então) A2 = x + 0 = x
substituindo 0 por 1, temos:

x + 1 = x (o que é um ABSURDO) Pois, x+1 = x+1.

E dessa forma, provamos por absurdo, que obrigatóriamente, 0 =/ 1.

HUhuhuu!! dahora, não? hahaha


Provando que Só Existe Um Único Numero com a Função de Zero

Estranho? É, realmente. Vamos provar que não existe dois zeros no universo dos números reais.

QUe doidera, não?

Bem, isso aconteceu na aula de Laboratório do prof. Simon. Todos começaram a dar risada. Eu logo disse que era uma coisa totalmente óbvia e absurda; sei lá, ele estava de gozação com a minha cara. E essas (obvias e absurdas) são as mais dificeis de provar, porque você não consegue pensar num problema, ou equação, já que você tem a resposta tão claramente na mente.
Mas o professor fez QUESTÃO de provar, para todos ficarem ridentes de inconformidade.

Vamos lá.

Provando;
Se temos um numero 0 (zero), então inventemos um outro, chamando de 0*

Vamos usar as propriedades do corpo.

Por A3 temos que:
x + 0 = x (I)
e que:
x + 0* = x (II)

então vamos dar o valor para x ---> x = 0
E novamente usemos a propriedade da A3 (II)

x + 0* = x
substitundo, temos:

0 + 0* = 0

então, assim percebemos, que esta, é a mesma que a (I), onde: x + 0 = x
Então, concluimos, que 0 = 0*, ou seja, se tratam da mesma referência(ponto, pessoa, numero etc.)

E assim, provamos, que só existe um unico numero (zero) que desempenha sua função na reta Real. E não dois, nem tres. E nem um outro numero imaginário qualquer. POrém, é possivel, inventarmos um outro numero, que também assuma a função de zero, mas não nos REais, nem nos N, Z, Q, R - Q e C... talvez, em algum outro conjunto já descoberto por alguem.

........

Parece bobo, ridiculo, intuito demais... nao? Bem, é o que eu penso. O intrigante é quando o professor diz: "Prove então". E você tem que provar racionalmente, e não por meras palavras. E depois, com o tempo, você percebe que uma das coisas mais divertidas que existem é provar coisas, tanto aquelas complexas, por indução que, as vezes, usa-se folhas e folhas de contas; como até essas mais simples e intuitivas.


Tente provar:

a) a/b = ac/bc
b) -a = (-1)a
c) a²=a.a ou (-a).(-a)

etc. Tente provar as coisas mais idiotas e absurdas que possam vir na sua mente. Por exemplo, tente provar que o céu é azul, que a água é molhada. E é sério, TEM COMO. E o mais legal é quando você consegue provar isso. Você sente um gozo inexprimivel de prazer ao descobrir tais. E ao mesmo tempo você desenvolve seu raciocinio, a lógica, seu poder argumentativo, de provar e contrariar as coisas. E talvez, o mais engraçado, de "confundir" as pessoas. haha


Bem é isso. APenas coloquei exemplos simples. Porém, tem uns muito chatos e complexos. Como:

Prove que sen(a-b) = sena.cosb - senb.cosa --> e olha, esse até que não é tão dificil.
Um outro mais chato que se tem que usar Indução, e até Binomio de Newton:
Prove que (a + b)³ = a³ + 3a²b + 3ab² + b³


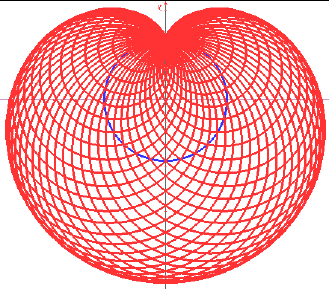
Uma coisa que também é muito legal que estou descobrindo, a partir de Função Limite e de Geometria Analitica. É que através das funções, podemos formar GRÁFICOS, Imagens, figuras, MUITO DAHORA!!! Maravilhosas, complexas, mas lógica, escrita por uma fórmula de tal modo que podemos manipular seus valores.
E essa é base da "engenharia" para construção de seus protótipos. Como a construção de uma PONTE ELEVADISSA, o formato dela, dos cabos de segunraça etc. É muito legal mesmo, quando vocÊ começa a fazer desenhos muito dahora, com seu lápis num papel, mas não porque de repente deu uma idéia na cabeça, mas sim, porque aquilo está dentro de uma fórmula racional. É algo maravilhoso. Veja um exemplo, do que se pode fazer, entre outros: